SPARGO: Exploring and Exploiting the Geometric Landscape of Infinite-Dimensional Sparse Optimization

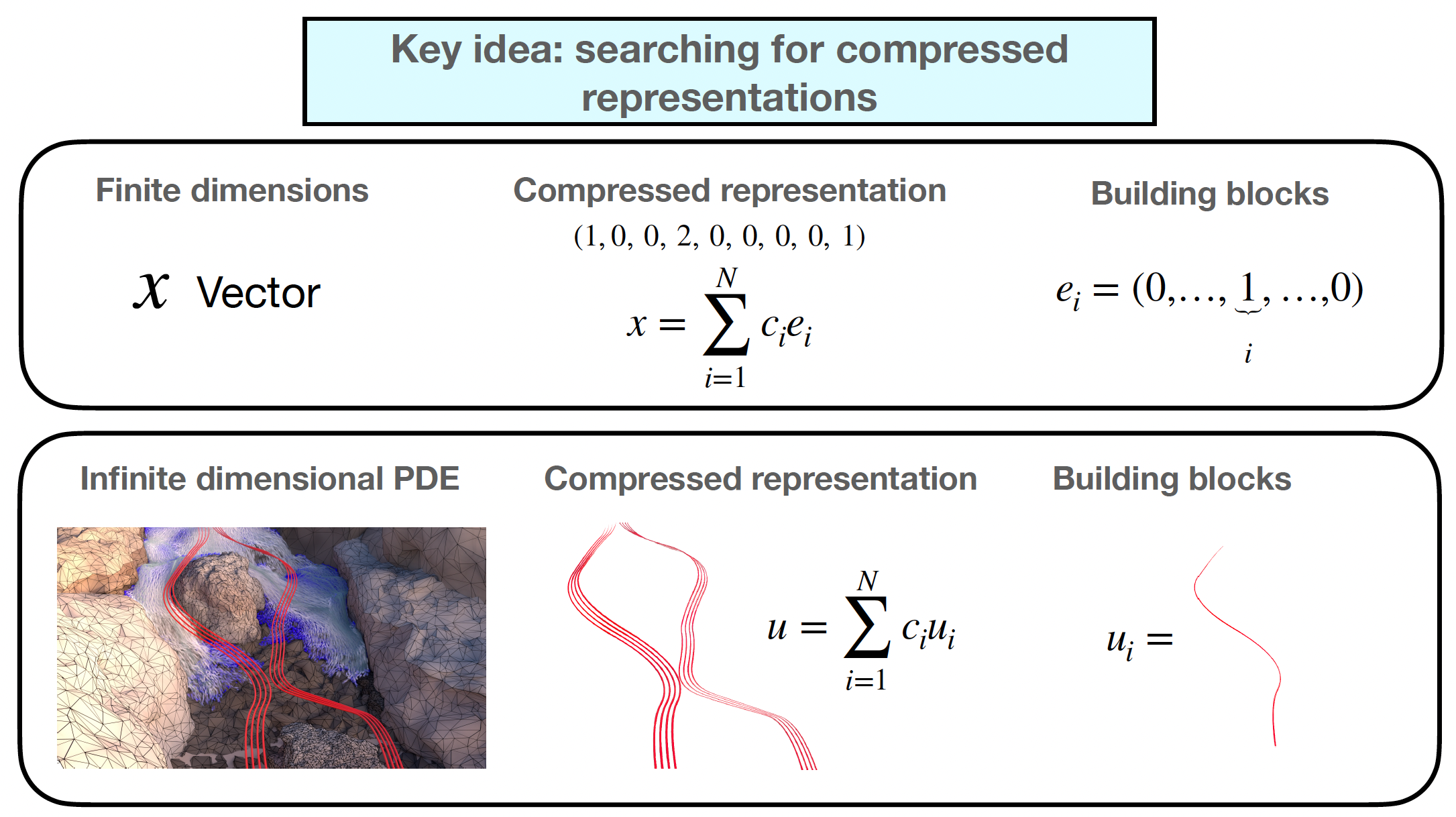
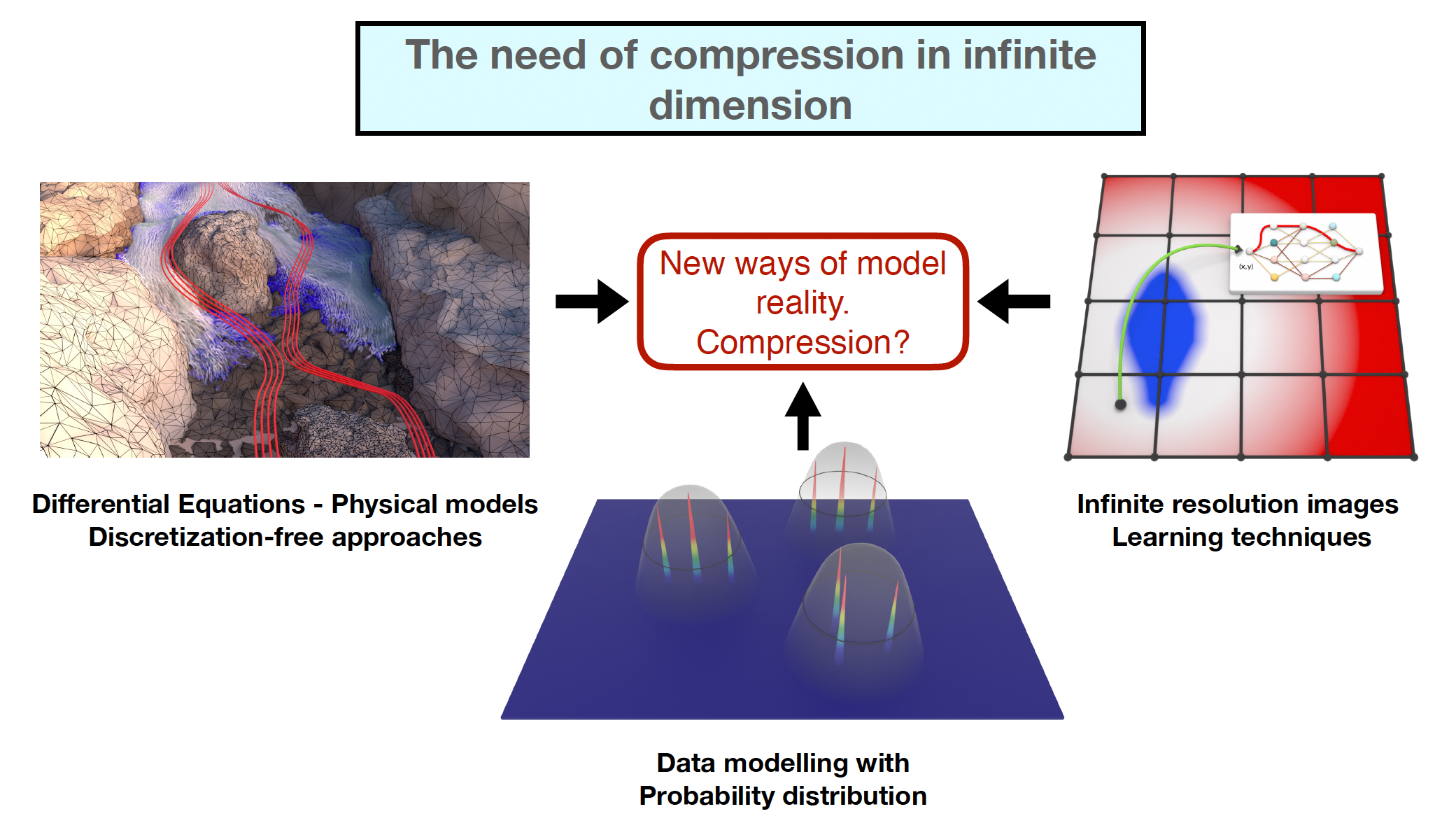
Summary: It is becoming clear that our society is overwhelmed by a growing flood of information, much of which is either redundant or unreliable. Even in our daily lives, we constantly face the challenge of filtering content from a variety of media. One way to tackle this challenge is through compression methods, which are already widely applied to finite-dimensional data. However, when it comes to infinite-dimensional structures which are often used to describe modern data, such methods remain unexplored. SPARGO aims to bridge this gap by developing a new framework for infinite-dimensional compression


SPARGO objectives:

• OB1: Sparse stability in infinite dimension.

  Is infinite-dimensional sparsity preserved under perturbations of the optimization problem? OB1 addresses this question by investigating how the ability to solve an optimization problem using only few building blocks is stable with respect to various types of perturbations.

• OB2: Analysis of Atomic Gradient Descents approaches.

  How can we use the sparse structure of infinite-dimensional optimization problems to design algorithms? The characterization of the sparse building blocks of a given optimization problem is instrumental to design algorithms that use such structure in the iterate. OB2 introduces a new class of infinite-dimensional sparse optimization algorithms named Atomic Gradient Descent methods that is built on such principle.